Red bayesiana para el problema de Monty Hall¶
Las redes bayesianas son modelos gráficos dirigidos que representan una probabilidad conjunta como producto de factores de probabilidades condicionales. Cada uno de los nodos de la gráfica se asocia a una variable $X_i$. Si una variable $X_j$ condiciona a otra variable $X_i$, entonces se crea una arista del nodo que representa a $X_j$ hacia el nodo que representa a $X_i$.
Esto permite simplificar el cálculo de diferentes probabilidades. Aquí, retomamos un problema probabilístico clásico: el problema de Monty Hall, el cual consiste en que un participante debe elegir 1 de 3 puertas (todas cerradas) de tal forma que éste recibirá como recompensa lo que esté detrás de la puerta. La idea es que en una de las puertas se encuentra un premio (un auto) y en las otras dos no los hay (se encuentran cabras). Así, el participante elige una puerta, pero antes de que se abra la puerta, el presentador, Monty Hall, elige otra puerta, donde sabe que no está el premio.
Creación de la red¶
Para crear una red Bayesiana para este problema determinaremos un conjunto de nodos que indexan las variables aleatorias del problema. Los nodos deben contar con:
- Nombre: indica la forma en que nos referiremos a cada variable dentro de la red.
- Padres: son los nodos que condicionan a la variable actual. Estos nodos son de suma importancia, pues determinan la estructura de la red.
- Tabla de probabilidad condicional: es la tabla de probabilidades que se asocia a la variable en el nodo; esta tabla especifica las probabilidades $p\big(X_i | \pi(X_i)\big)$ donde $\pi(X_i)$ son los padres de la variable $X_i$.
import numpy as np
class Node(object):
"""Clase para nodos en la red bayesiana"""
def __init__(self, name, cpt, parents=None):
#Se asigna un nombre de variable
self.name = name
#Se determinan sus padres (condiciones)
self.parents = parents
#Se asigna la tabla de probabilidad condicional de la variable
self.cpt = cpt
def __str__(self):
return "{}\n{}".format(self.name, self.cpt)
Una vez que tenemos la estructura de los nodos, construiremos la red bayesiana con base en la siguiente configuración:
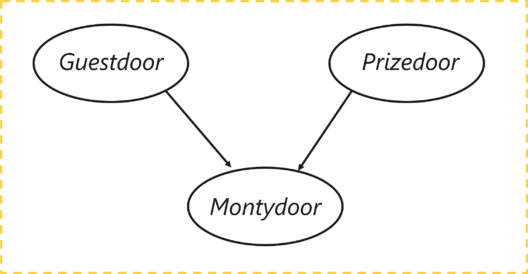
Contamos con tres variables:
- $X_0$: la variable que corresponde a la puerta elegida por el participante.
- $X_1$: la variable que corresponde a la puerta que contiene el premio, y que es conocida por Monty, el presentador.
- $X_2$: la variable que elige el presentador Monty, en el conocimiento de que sabe dónde está el premio.
Las variables $X_0$ (guestDoor) y $X_1$ (prizeDoor) son independientes entre sí, pero ambas condicionan a la elección que hará el presentador, es decir, el presentador elegirá una puerta en dónde sabe que no está el premio, y que no ha elegido el invitado.
Por tanto, tenemos las probabilidades:
- $p(X_0 = d_0)$, donde $d_0 =0,1,2$, es la probabilidad de que el participante elija una de las 3 puertas. En todo caso, la probabilidad es de $\frac{1}{3}$.
- $p(X_1 =d_1)$, donde $d_1 =0,1,2$, es la probabilidad de que el premio se encuentre detrás de la puerta $d$. Cada puerta tiene probabilidad de $\frac{1}{3}$ de contener al premio.
- $p(X_2 = d_2 | X_0 =d_0, X_1= d_1)$ que es la probabilidad de que el presentador, Monty, elija una puerta dado los padres, es decir, dado que el invitado a elegido una puerta $d_0$, y dado que el premio se encuentra en la puerta $d_1$. En este caso, la probabilidad se puede determinar por las elecciones. Si el premio esta en una puerta $d_1$ y el invitado ha elegido $d_0$ entonces la probabilidad de elegir alguna de estas puertas es 0. Si las puertas son las mismas $d_0 = d_1$, entonces cada una de las puertas restantes tiene probabilidad de 0.5. Finalmente, si $d_0 \neq d_1$, la probabilidad de que Monty elija la puerta restante es 1.
Además, definimos algunas funciones de utilidad:
- get_probs: Que da la probabilidad de una variable dado un valor.
- consult: Regresa la probabilidad de una consulta, es decir de una asignación $X_0 =d_0, X_1 =d_1, X_2= d_2$
class MontyNetwork(object):
"""Red Bayesiana para el problema de Monty Hall"""
def __init__(self):
#Variables nodos
self.X0 = Node(name='guestDoor', cpt=[1/3, 1/3, 1/3])
self.X1 = Node(name='prizeDoor', cpt=[1/3, 1/3, 1/3])
self.X2 = Node(name='montyDoor', parents=[self.X0, self.X1],
cpt=np.array([[[0,0,0],[0.5,0,1],[0.5,1,0]],
[[0,0.5,1],[0,0,0],[1,0.5,0]],
[[0,1,0.5],[1,0,0.5],[0,0,0]]]))
def get_probs(self, var, value):
"""Obtiene la probabilidad de una Variable en base a su valor"""
if var == 'guestDoor':
return self.X0.cpt[value]
elif var == 'prizeDoor':
return self.X1.cpt[value]
elif var == 'montyDoor':
return self.X2.cpt[:,value,:]
def consult(self, guest=0, prize=0, monty=0):
"""Da la probabilidad de una consulta, donde las 3 variables tienen valores"""
p_guest = self.get_probs('guestDoor', guest)
p_prize = self.get_probs('prizeDoor', prize)
p_monty = self.get_probs('montyDoor', monty)[prize][guest]
return p_monty*p_prize*p_guest
Creamos la red Bayesiana para el problema de Monty Hall:
#Guarda la estructura de red Bayesiana
bn = MontyNetwork()
Podemos consultar, las probabilidades de que cada variable tome un valor específico:
print('Probabilidades para monty = 0: \n{}\n'.format(bn.get_probs('prizeDoor', 0)))
print('Probabilidades para monty = 1: \n{}'.format(bn.get_probs('montyDoor', 1)))
Probabilidades para monty = 0: 0.3333333333333333 Probabilidades para monty = 1: [[0.5 0. 1. ] [0. 0. 0. ] [1. 0. 0.5]]
Y podemos realizar una consulta. Recuérdese que la probabilidad de una consulta es de la forma:
$$p(X_0 =x_0, X_1 = x_1, \cdots, X_n = x_n) = \prod_{i=0}^n p\big(X_i = x_i | \pi(X_i)\big)$$
Que en este caso tiene la forma:
$$p(X_0 =d_0, X_1= d_1, X_2=d_2) = p(X_2 = d_2 | X_0=d_0, X_1=d_1)p(X_1=d_1) p(X_0 = d_0)$$
#Consulta
cons = [0,2,1]
#Probabilidad conjunta de una consulta
prob = bn.consult(guest=cons[0], prize=cons[1], monty=cons[2])
print('Probabilidad de la consulta X1={},X2={},X_3={}: {}'.format(cons[0],cons[1],cons[2], prob))
Probabilidad de la consulta X1=0,X2=2,X_3=1: 0.1111111111111111
De igual forma, podemos calcular la probabilidad de las variables. En este caso, por ejemplo, no conocemos la probabilidad marginal de la variable $X_2$ correspondiente a la elección de Monty. En este caso, la probabilidad está determinada de la forma:
$$p(X_2 = d_2) = \sum_{d_0} \sum_{d_1} p(X_0 =d_0, X_1= d_1, X_2=d_2) $$
Definimos una función que calcule esto para cada uno de los posibles valores de $d_2$, por lo que nos regresará un vector con 3 entradas.
def prob_monty(bn):
"""Obtiene la probabilidad total de la variable monty"""
total_prob = 0
for i in [0,1,2]:
for j in [0,1,2]:
total_prob += bn.X2.cpt[i,:,j]*bn.X1.cpt[i]*bn.X0.cpt[j]
return total_prob
print('Probabilidades de X2: \n{}'.format(prob_monty(bn)))
Probabilidades de X2: [0.33333333 0.33333333 0.33333333]
Como podemos observar, la probabilidad de que Monty elija cada una de las puertas es $\frac{1}{3}$, lo que no es de extrañar. Pues en principio esta probabilidad no cuenta con ninguna otra información. Lo que nos interesa ahora es saber qué pasa cuando tenemos información de otras variables. Principalmente, nos interesa saber qué pasa con la variable del premio. Si conocemos que el invitado y monty han hecho una elección ¿en dónde es más probable que se encuentre el premio.