Algoritmo Naïve Bayes¶
El algoritmo de Bayes naïve (o ingenuo) es un modelo gráfico dirigido, que entra dentro de la familia de las redes bayesianas. De hecho, puede pensarse como una red bayesiana bastante simple donde se tiene un vector de evidencias $x = \begin{pmatrix} x_1 & x_2 & \cdots & x_d \end{pmatrix}$ y una variable $Y$ sobre la que queremos obtener una consulta, su probabilidad.
El algoritmo de Bayes naïve puede considerarse como un algoritmo de clasificación, en tanto con la estimación de la probabilidad realizada, puede eligir el valor $y_i$ de la variable $Y$ que maximiza la probabilidad de la evidencia. Este valor de probabilidad máxima se dice que es la clase del vector $x$.
Presentamos una implementación del algoritmo de Bayes naïve para un problema particular que la clasificación de texto en lenguas a partir de la frecuencia de los conjuntos de caracteres que en ellos se presentan.
from nltk.corpus import brown, cess_esp
from nltk import ngrams
from elotl.corpus import load
from itertools import chain
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from collections import Counter, defaultdict
from re import sub
import numpy as np
Preparación de los datos¶
En primer lugar, obtenemos los datos con los que vamos a trabajar. Para esto utilizamos dos paqueterías que cuentan con datos textuales en diferentes lenguas:
- NLTK (Natural language toolkit): Es una paquetería que cuenta con diferentes conjuntos de datos textuales. En particular usamos dos:
- Brown corpus: es un conjunto de datos con textos en inglés.
- Cess corpus: es un conjunto de datos con textos en español.
- Elotl: Es una paquetería que cuenta con datos textuales para conjuntos de datos en lenguas indígenas habladas en México; en particular tomamos dos:
- Tsunkua corpus: conjunto de datos textuales para el otomí.
- Axolotl corpus: conjunto de datos textuales para el náhuatl.
#Datos a usar en inglés, español, otomí y náhuatl
eng = brown.sents()
esp = cess_esp.sents()
oto = [sent[1].split() for sent in load('tsunkua')]
nah = [sent[1].split() for sent in load('axolotl')]
Para hacer la clasificación usaremos conjuntos de caracteres (n-gramas); es decir, un texto se clasificará en una lengua según los patrones de caracteres que contenga. En este caso, podemos pensar un n-grama como la creación de un conjunto de subcadenas de tamaño n, a partir de la cadena completa.
Por ejemplo, si pensamos en la palabra "gato" y usamos $n=2$ (2-gramas o bigramas), tenemos que la función de get_ngrams realizará lo siguiente:
$$gato \mapsto \{ga, at, to\}$$
Es decir, obtiene tres elementos que corresponde a subcadenas de longitud $n=2$. Estas subcadenas se obtienen al tomar una ventana de tamaño $n$ que recorre la cadena.
Hacemos esto puesto que nuestro objetivo es detectar de que idioma se trata. Obtener estos patrones de caracteres nos permite detectar con alto grado de precisión la lengua.
def get_ngrams(word,n):
"""Función para obtener n-gramas."""
#Limpia el texto
clean_word = sub('[^\w\s)]','',word.lower())
if len(clean_word) <= n and clean_word != '':
#Si no se peuden obtener n-gramas
ngram_list = [clean_word]
else:
#Obtiene n-gramas
ngram_list = [''.join(ngram) for ngram in ngrams(clean_word,n)]
return ngram_list
def process(sent, n=2):
"""Función para procesar las oraciones de un texto."""
sent_ngrams = list(chain(*[get_ngrams(w,n) for w in sent]))
return sent_ngrams
Podemos observar qué tipo de procesamiento es el que se hace para una cadena con varias palabras:
input_text = 'y el ¿que del niño de aquí?.'.split()
print(process(input_text))
['y', 'el', 'qu', 'ue', 'de', 'el', 'ni', 'iñ', 'ño', 'de', 'aq', 'qu', 'uí']
Generación del conjunto de datos¶
Definiremos una clase que nos permitirá manejar el conjunto de datos de manera simple. Lo que hace esta clase es:
- Guarda las clases (lenguas) que consideramos para clasificar.
- Genera los n-gramas de los textos de los conjuntos de datos que hemos exportado anteriormente.
- Asocia cada uno de los n-gramas a las lenguas (clases).
class Dataset(object):
"""Clase para crear el dataset de las lenguas."""
def __init__(self):
#Lenguas a considerar
self.languages = {'english': eng,'spanish':esp,'nahuatl':nah,'otomi':oto}
self.X = []
self.Y = []
def get_dataset(self):
"""Función para crear el dataset (pares [x,y]) a partir de los textos."""
for lang, sentences in self.languages.items():
print(lang)
for sent in sentences:
#Procesa los textos
x = process(sent)
#Genera los inputs y las clases
self.X.append(x)
self.Y.append(lang)
#Creamos el dataset
dataset = Dataset()
dataset.get_dataset()
english
spanish nahuatl otomi
Podemos observar de que tamaños son los datos que tenemos; es decir, cuántas evidencias podemos usar para estimar las probabilidades del modelo de bayes naïve. Aquí $X$ corresponde a las evidencias y $Y$ a las clases que se asocian con cada una de las evidencias. El conjunto de datos es un conjunto de pares:
$$\mathcal{S} = \{(x,y) : x \text{ es evidencia}, y \text{ es clase}\}$$
#Imprime longitud del dataset
print(len(dataset.X), len(dataset.Y))
84450 84450
Finalmente, separaremos el conjunto de datos en dos partes. Esta partición la hacemos de forma aleatoria, y conformamos los dos conjuntos:
- Conjunto de entrenamiento: Refiere a los datos que nos van a servir para estimar las probabilidades del modelo de bayes ingenuo. Corresponde a un 70% de los datos totales.
- Conjunto de evaluación: Estos datos nos servirán para poder evaluar qué también trabaja nuestro modelo. Corresponde al 30% de los datos totales. Si nuestra evaluación es satisfactoria, podemos integrar esta parte de los datos a los de entrenamiento para hacer una estimación más completa del modelo.
Para hacer esta separación, utilizamos la función train_test_split de la paquetería sklearn.
# Separación de los datos
x_train, x_test, y_train, y_test = train_test_split(
dataset.X, dataset.Y, test_size=0.3, random_state=123
)
Modelo de Bayes Naïve¶
Ahora definimos el modelo de Naïve Bayes con el cual podremos realizar la clasificación que esperamos. Como señalamos, el modelo de Bayes naïve es una red bayesiana con la siguiente estructura:
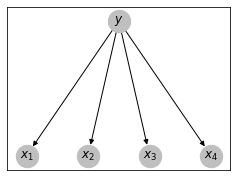
Como se ve en la gráfica, se tiene un conjunto de variables $X_1, X_2,...,X_d$ que son independientes entre sí; es decir, no tienen ninguna arista que conecte alguna variable $X_i$ con otra $X_j$. De hecho, el nombre de naïve o ingenuo del método proviene precisamente en asumir que las observaciones o evidencia son independientes entre sí.
Al mismo tiempo, podemos observar que cada $X_i$ tiene un único nodo padre que es la variable $Y$; es decir, $Y$ genera la evidencia (de allí también que se le conozca como un modelo generativo). De esta forma tenemos que para toda $i \in \{1,2,...,d\}$ se tiene que:
$$p\big(X_i | \pi(X_i) \big) = p(X_i | Y)$$
El caso de la variable $Y$, como no cuenta con padres, sabemos que solo debemos estimar la probabilidad $p(Y)$ para cada valor posible de $Y$. Nuestro objetivo es estimar la probabilidad conjunta $p(Y=y,X_1=x_1,...,X_d=x_d)$ dada una evidencia $x = \begin{pmatrix} x_1 & \cdots & x_d \end{pmatrix}$. Por lo que sabemos de las redes bayesianas, esta probabilidad conjunta se estima como:
$$p(Y=y,X_1=x_1,...,X_d=x_d) = p(Y=y)\prod_{i=1}^d p(x_i|y)$$
También podemos calcular la probabilidad condicional; esto es, estimar:
$$p(Y=y|X_1=x_1,...,X_d=x_d) = \frac{p(Y=y)\prod_{i=1}^d p(x_i|y)}{\sum_y p(Y=y)\prod_{i=1}^d p(x_i|y)}$$
Sin embargo, como lo que queremos encontrar, en general, es la clase $y$ a la que pertenece el vector $x$ esto no es necesario, pues podemos ver que la clase con mayor probabilidad $\hat{y}$ se obtienen como:
$$\hat{y} = \arg\max_y p(Y=y|X_1=x_1,...,X_d=x_d) = \arg\max_y p(Y=y,X_1=x_1,...,X_d=x_d)$$
Por lo que, en general, sólo estimaremos la probabilidad conjunta. A continuación construimos una clase para el modelo de clasificación de Bayes Naïve. En este caso, las tablas de probabilidad condicional que responden a las probabilidades $p(Y)$ y $p(X|Y)$ se estiman de manera frecuentista. En concreto:
- $p(Y=y) = \frac{frec(y)}{\sum_y frec(y)}$
- $p(X_i=x_i|Y=y) = \frac{frec(x_i, y)}{frec(y)}$
Donde $frec(\cdot)$ es la frecuencia de ese ítem. Las funciones que definimos son las siguientes:
- fit: Estima las probabilidades del modelo; es decir, obtiene las tablas de probabilidad para cada variable. En este caso $p(X|Y)$ y $p(Y)$.
- predict_proba: Obtiene la probabilidad conjunta $p(Y=y, X_1=x_1, ...,X_d=x_d)$ para cada una de las clases $y$ dado un vector de evidencia $x$.
- predict_logproba: Sustituye las probabilidades por el logaritmo de las probabilidades para cambiar la estimación de productos por sumas (evitando así el desvanecimiento de probabilidades muy pequeñas): $$\log p(Y=y,X_1=x_1,...,X_d=x_d) = \log p(Y=y)+ \sum_{i=1}^d \log p(x_i|y)$$
- predict: con base en el logaritmo de la probabilidad o a la probabilidad, regresa la clase que maximiza el valor. La clase más probable.
class NaiveBayesClassifier(object):
"""Clase del modelo de bayes ingenuo."""
def __init__(self, priors={}):
#Prior, p(Y)
self.prec_priors = priors
self.priors = {}
#Clases a considerar
categories = []
#Condicionales, p(X|Y)
self.conditional = {}
def count_cat(self, y):
"""Función para contar las clases."""
freqs = Counter(y)
total_freq = sum(freqs.values())
for lang, freq in freqs.items():
self.priors[lang] = freq/total_freq
def count_cond(self,x,y):
"""Función para contar las probabilidades condicionales p(x|y)"""
freq_cat = Counter(y)
print(freq_cat)
joint_elements = defaultdict(list)
for category,example in zip(y,x):
joint_elements[category].append(example)
for category,examples in joint_elements.items():
freqs = Counter(chain(*examples))
total_freq = sum(freqs.values())
self.conditional[category] = {w:freq/total_freq for w,freq in freqs.items()}
def fit(self,x,y):
"""Función para entrenar el modelo. Estimar las probabilidades."""
if self.prec_priors == {}:
self.count_cat(y)
else:
for i,category in enumerate(set(y)):
self.priors[category] = self.prec_priors[i]
self.categories = list(self.priors.keys())
self.count_cond(x,y)
def predict_proba(self,x):
"""Función para obtener probabilidades de clases. Para cada clase y, obtiene p(y,x1,...,xd)"""
prediction = np.zeros(len(self.priors))
for i,category in enumerate(self.categories):
p = 1
prior = self.priors[category]
for x_i in x:
try:
cond = self.conditional[category][x_i]
except:
cond = 1/prior
p *= cond*prior
prediction[i] = p
return prediction
def predict_logproba(self,x):
"""Función para obtener logaritmos de probabilidades de clases."""
prediction = np.zeros(len(self.priors))
for i,category in enumerate(self.categories):
p = 0
prior = self.priors[category]
for x_i in x:
try:
cond = self.conditional[category][x_i]
except:
cond = 1/prior
p += np.log(cond*prior)
prediction[i] = p
return prediction
def predict(self,x,log=True):
"""Función para predecir las clases de un ejemplo de evaluación."""
if log:
probas = self.predict_logproba(x)
else:
probas = self.predict_proba(x)
y_hat = np.argmax(probas)
#print(self.categories)
#print(probas)
return self.categories[y_hat]
Aplicación del modelo a los datos¶
Construimos el modelo en base a unos priors uniformes, pues asumimos que la distribución de las lenguas es la misma en cada caso (cada lengua tiene la misma probabilidad de suceder independientemente de las evidencias) y lo entrenamos con nuestros datos de entrenamiento que hemos obtenido anteriormente. Se imprime el número de datos observados en cada lengua para hacer la estimación.
#Modelo
clf = NaiveBayesClassifier(priors=[0.25,0.25,0.25,0.25])
#Entrenamiento
clf.fit(x_train,y_train)
Counter({'english': 40160, 'nahuatl': 11210, 'spanish': 4267, 'otomi': 3478})
Podemos ver cómo se comporta el modelo. Al tener activada la opción log (log=True) los valores serán logarítmicos, por lo que el método regresa valores negativos. La función imprimirá las probabilidades logarítmicas para cada lengua y regresará la clase con mayor probabilidad.
#Texto de entrada
input_text = 'hello'
#Imprime la clase
print('La lengua más probable es: {}'.format(clf.predict(process(input_text.split()), log=True)))
La lengua más probable es: english
Por ejemplo, si tomamos un texto en español obtenemos:
#Texto de entrada
input_text = 'hola' #'ra detha' #'tinechmacasnequi'
#Imprime la clase
print('La lengua más probable es: {}'.format(clf.predict(process(input_text.split()), log=True)))
La lengua más probable es: spanish
Si tomamos otra lengua, también podemos ver los valores que arrojan. En este caso, usamos log=False, por lo que regresa probabilidades no logarítmicas:
#Texto de entrada
input_text = 'ra detha' #'tinechmacasnequi'
#Imprime la clase
print('La lengua más probable es: {}'.format(clf.predict(process(input_text.split()), log=False)))
La lengua más probable es: otomi
Evaluación del modelo¶
Para evaluar el modelo, usamos el dataset de evaluación y predecimos las clases a las que pertenece. Calculamos métricas de evaluación para saber qué tan bien trabaja nuestro modelo.
y_pred = [clf.predict(x) for x in x_test]
print(classification_report(y_test, y_pred))
precision recall f1-score support
english 0.89 0.94 0.91 17180
nahuatl 0.97 0.87 0.91 4907
otomi 0.41 0.52 0.46 1485
spanish 0.60 0.34 0.43 1763
accuracy 0.86 25335
macro avg 0.72 0.67 0.68 25335
weighted avg 0.86 0.86 0.85 25335
En este caso, podemos ver que el accuracy es de 0.86; es decir, que acierta en el 86% de los casos. Podemos ver cómo trabaja en casos individuales de clasificación. Finalmente, podemos explorar cuáles son los rasgos que más influyen para la decisión en cada una de las clases:
from operator import itemgetter
sorted(clf.conditional['english'].items(),key=itemgetter(1),reverse=True)[:50]
[('th', 0.03560876240584964),
('he', 0.03263565260758265),
('in', 0.023582226280286698),
('er', 0.020115293227803567),
('an', 0.019262873682196296),
('re', 0.01772942252436722),
('on', 0.0163530455824101),
('at', 0.014116715559312279),
('en', 0.01380558054178174),
('nd', 0.012901932954547167),
('ed', 0.012405849639670995),
('es', 0.012276649505272722),
('or', 0.012221654695878704),
('ti', 0.011430256788092192),
('te', 0.011341737745574424),
('is', 0.011051696627537484),
('it', 0.011009885505326963),
('st', 0.01095903414047633),
('to', 0.010856578057221723),
('ar', 0.010469731007580243),
('of', 0.010392512268362616),
('ng', 0.01011490148395583),
('ha', 0.009954060500317162),
('nt', 0.009930329863386867),
('al', 0.009898689014146473),
('ou', 0.009631248502709813),
('as', 0.00928545922172551),
('hi', 0.008614974559250504),
('se', 0.008497828081705712),
('le', 0.008407425655304588),
('ve', 0.00812115130503436),
('me', 0.00789024844093482),
('co', 0.007438989662482541),
('de', 0.007305646083540882),
('ne', 0.0072954758105707555),
('ro', 0.007207710121606331),
('ea', 0.0071941497576461615),
('io', 0.006806926031228011),
('ri', 0.006623107764212392),
('ic', 0.006378267859376012),
('ll', 0.00633871679782552),
('ra', 0.006208763309873903),
('a', 0.006137571399083018),
('li', 0.0061149707924827365),
('ce', 0.005997824314937946),
('be', 0.005913825393740235),
('ch', 0.005759011238528309),
('om', 0.005458799847521241),
('ma', 0.005449382928104457),
('el', 0.005350316935839892)]