Redes neuronales para secuencias¶
En el procesamiento del lenguaje natural (PLN), el procesamiento de secuencias es esencial en tanto que las cadenas del leguaje (principalmente texto) están determinados por este tipo de estructura. Podemos pensar estos datos como dependientes del tiempo $x^{(1)} x^{(2)} \cdots x^{(T)}$; esto es, como procesos estocásticos. Para trabajar con este tipo de datos se requieren de redes neuronales que puedan trabajar con esta estructura dentro de los datos.
Modelos secuenciales. Una red neuronal para secuencias toma como entrada un conjunto de datos secuenciales $x^{(1)} x^{(2)} \cdots x^{(T)}$ y cuya salida se estima como: $$f(x^{(1)} x^{(2)} \cdots x^{(T)}) = \phi\big(W^{(out)} h^{(1:t)} + b^{(out)}\big)$$ donde $h^{(1:t)}$ es una representación profunda de los datos de entrada, $\phi$ es la función de activación en la salida y $W^{(out)}$ y $b^{(out)}$ los pesos y el bias en la salida, respectivamente.
Un ejemplo de este tipo de modelos son las redenes neuronales recurrentes que puede definirse como:
Red neuornal recurrente. Es una red que representa los datos secuenciales como: $$h^{(t)} = g(Wh^{(t-1)} + W'x^{(t)} + b)$$
Las redes recurrentes se utilizan para generar modelos que transformen una secuencia en otra secuencia a partir de una arquitectura encoder-decoder:
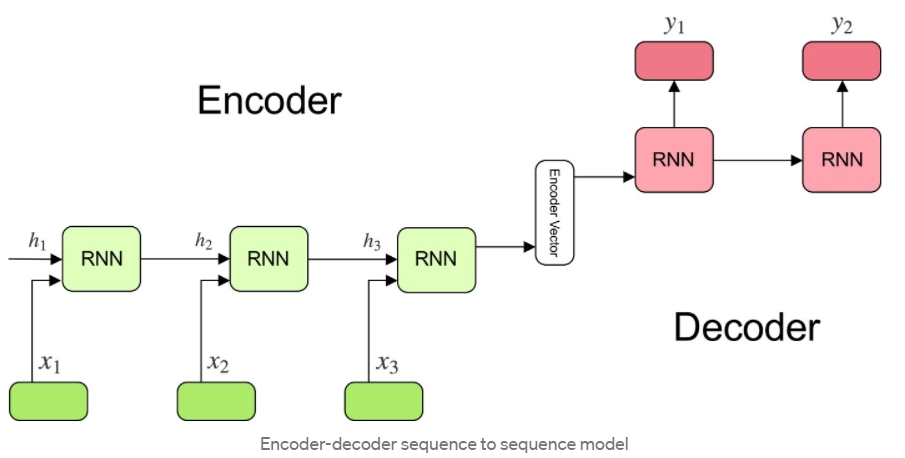
La codificación del encoder son los vectores $h^{(1)} h^{(2)} \cdots h^{(T)}$ son utilizados para crear un vector de codificación que pasa hacia el decoder para obtener las salidas. Sin embargo, este procedimiento toma la codificación completa de la entrada para obtener todos los elementos de la secuencia de salida.
Atención en redes recurrentes¶
Para solventar esto último, Bahdanau, Cho y Bengio (2014) introducen el mecanismo de atención. Este mecanismo se basa en enfocarse (poner "atención") en las entradas que tengan mayor influencia en la salida actual. De manera esquemática, la atención en las redes recurrentes se computa de la siguiente forma:
- Se calculan las representaciones del encoder $h^{(1)} h^{(2)} \cdots h^{(T)}$.
- Por cada representación de la salida $s^{(t)}$ en el tiempo $t$ se estiman los scores como: $$sc_{t,k} = e(s^{(t-1)}, h^{(k)})$$ donde $e$ es una función de similitud.
- Se estima la probabilidad softmax sobre los valores de entrada, estos son los pesos de atención: $$\alpha_{t,k} = Softmax\big( sc_{t,k} \big)$$
- Finalmente, se obtiene el vector de contexto $c^{(t)}$ a partir de la suma ponderada de las representaciones de la entrada por los pesos de atención: $$c^{(t)} = \sum_{k=1}^T \alpha_{t,k} h^{(k)}$$
Visualmente, se puede representar este proceso de atención como:
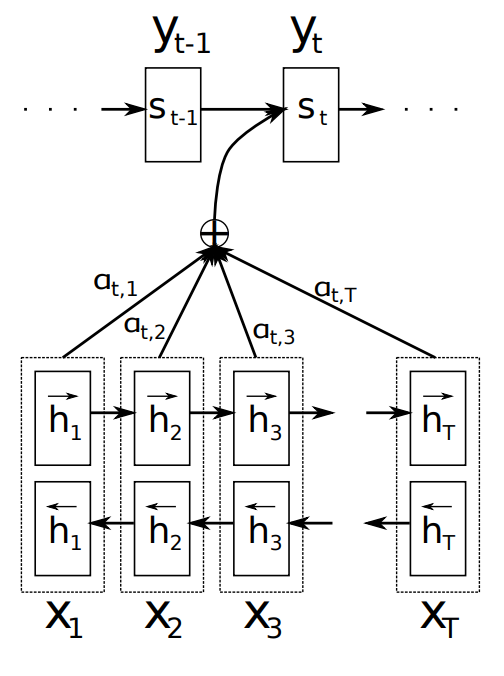
La función $e()$ para el cálculo de los scores puede determinarse de las siguientes maneras:
- Producto punto: $$sc_{t,k} = s^{(t-1)} \cdot h^{(k)}$$
- Forma bilineal: (Luong et al, 2015) Dada una matriz de pesos $W$: $$sc_{t,k} = s^{(t-1)} W h^{(k)}$$
- MLP: (Bahdanau et al, 2014) Dada una matriz de pesos $W$ y un vector de pesos $v$: $$sc_{t,k} = v^T\tanh(W[s^{(t-1)}; h^{(k)} + b])$$
A partir de estos modelos, la atención demostró tener un potencial importante en las aplicaciones de PLN y dieron pie las arquitecturas de Transformadores.
Referencias¶
Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
Luong, M. T., Pham, H., & Manning, C. D. (2015). Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025.