Auto-atención¶

La auto-atención (self-attention) ha tenido un gran impacto en el desarrollo actual de la lingüística computacional. Este tipo de atención es introducido por Vaswani et al.(2018) dentro de la arquitectura de transformador que proponen. La auto-atención tiene los mismos principios de la atención, pero realizada entre los elementos de un mismo conjunto.

Pesos de auto-atención: Si $x_1, x_2, ... x_n \subseteq \mathbb{R}^d$ es un conjunto de vectores, los pesos de auto-atención se determinan por medio de la función $\alpha: \mathbb{R}^d \times \mathbb{R}^d \to (0,1)$ como: $$\alpha(x_i, x_j) = Softmax\Big( \frac{\psi_k(x_i)^T \psi_q(x_j)}{\sqrt{d}} \Big)$$ donde $\psi_q$ y $\psi_k$ son proyecciones de los puntos.

Los pesos de atención pueden verse como probabilidades condicionales que determinan la "similitud" de los puntos. Esta "similitud" está determinada por el producto punto escalado. Las proyecciones que se realizan sobre los datos suelen ser proyecciones lineales:

$$\psi_q(x_i) = W_q x_i \\ \psi_k(x_i) = W_k x_i$$

En estas proyecciones, $W_q, W_k \in \mathbb{R}^{d\times d}$ son matrices de parámetros que se aprenden durante el entrenamiento de la red neuronal. Si las proyecciones son lineales, podemos observar que:

$$\alpha(x_i, x_j) = Softmax\Big( \frac{x_i^T W_k^T W_q x_j}{\sqrt{d}} \Big) \\ = Softmax\Big( \frac{x_i^T W x_j}{\sqrt{d}} \Big)$$

con $W = W_k^T W_q$. El producto punto escalado busca encontrar una relación de similitudentre las entradas que, además, considere las proyecciones de los datos. Es decir, en lugar de estimar una similitud basado en una relación lineal (producto punto), los datos se proyectan en un espacio de queries y en un espacio de keys para determinar la similitud entre los datos en estos dos espacios:

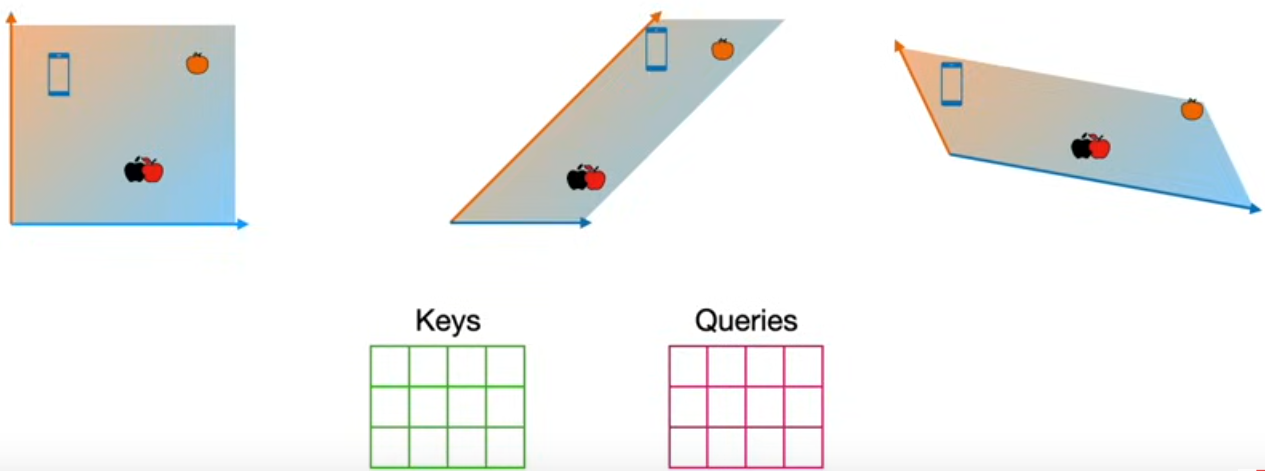
Los pesos de atención ponderan los datos $x_1, ..., x_n$ para obtener una nueva representación de cada dato $x_i$, $i \in \{1,2,...,n\}$. Por ejemplo, si denotamos como $h_i$ a la representación del vector $x_i$, entonces esta representación se obtiene como:

$$h_i = \sum_{j=1}^n \alpha(x_i, x_j) \psi_v(x_j)$$

De igual forma, la función $\psi_v$ es una proyección de $x_j$ que generalmente se realiza de forma lineal:

$$\psi_v(x_j) = W_v x_j$$

Como se puede ver en la fórmula, la auto-atención obtiene una representación de la entrada con base en una combinación convexa de todos los elementos de la entrada. Los elementos que tienen una mayor influencia dentro de la representación de ese dato. Entre mayor sea el peso de atención, hay una mayor influencia para su representación. Por ejemplo, los siguientes pesos de atención muestran los elementos que mayor influencia tienen en la representación de cada palabra:

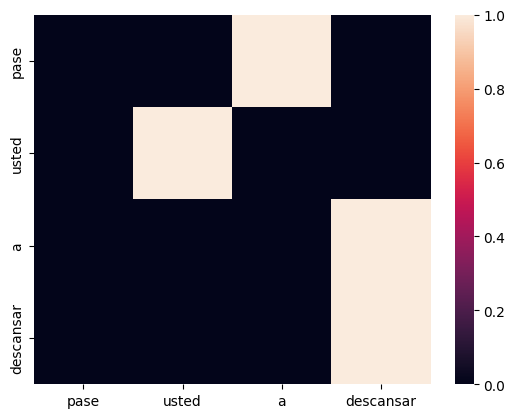
Las operaciones de la auto-atención pueden expresarse en notación matricial. Si $X\in\mathbb{R}^{n\times d}$ es la matriz cuyos renglones son los vectores $x_1, x_2,...,x_n$, entonces podemos expresar la auto-atención de la siguiente forma:

$$Att(Q,K,V) = Softmax\Big( \frac{QK^T}{\sqrt{d}} \Big) V$$

Donde:

$$Q = XW_q^T \\ K = XW_k^T \\ V = XW_v^T$$

De tal forma que $Att(Q, K, V)$ es una matriz cuyos renglones son las representaciones de los datos de entrada. Es decir:

$$Att(Q, K, V)_i = \sum_{j=1}^n \alpha(x_i, x_j) \psi_v(x_j) \\ = \sum_{j=1}^n Softmax\Big( \frac{x_i^T W_k^T W_q x_j}{\sqrt{d}} \Big) W_v x_j$$

Implementación¶

La implementación de para la auto-atención en PyTorch se puede realizar de manera sencilla:

Se generan tres matrices de parámetros por medio del uso de capas líneales sin incluir el bias. Estas tres matrices representan a $W_q$, $W_k$ y $W_v$ (query, key y value, respectivamente).
En el forward se proyectan los datos en cada matriz $Q$, $K$ y $V$.
Se computan los scores como $\frac{QK^T}{\sqrt{d}}$ y se aplica la función softmax para obtener los mesos de atención.
Se multiplica la matriz de pesos de atención por la matriz $V$ para obtener las representaciones finales.

Nuestra implementación de auto-atención regresa tanto las salida de representaciones de los datos, como la matriz de atención.

class SelfAttention(nn.Module):
    def __init__(self, d_model):
        super(SelfAttention, self).__init__()
        # Capas de proyecciones
        self.d_model = d_model
        self.Q = nn.Linear(d_model, d_model, bias=False)
        self.K  = nn.Linear(d_model, d_model, bias=False)
        self.V  = nn.Linear(d_model, d_model, bias=False)

    def forward(self, x):
        # Proyección de los datos
        query,key,value = self.Q(x),self.K(x),self.V(x)
        # Cálculo de pesos de atención
        scores = torch.matmul(query, key.T)/np.sqrt(self.d_model)
        p_attn = torch.nn.functional.softmax(scores, dim = -1)
        #Suma ponderada
        Vs = torch.matmul(p_attn, value).reshape(x.shape)

        return Vs, p_attn

Antes de probar la matriz de atención, definiremos otros módulos para realizar de manera adecuada su aplicación sobre las cadenas del lenguaje natural.

Auto-atención¶

Implementación¶

Referencias¶