Auto-atención y estructura de los datos¶
La auto-atención busca obtener, a partir de un conjunto de elementos de entrada $x_1, x_2, ..., x_n$, una representación $h_1, h_2,...,h_n$ que codifique las relaciones que existen entre los elementos de entrada. Estas relaciones se codifican en los pesos de atención $\alpha(x_i, x_j)$. Como otros modelos de aprendizaje profundo, lo que se busca con la auto-atención en los tranformadores es obtener una representación de los datos de entrada que permita realizar la tarea a la que se orienta la arquitectura; es decir, es parte del aprendizaje representacional.
Auto-atención como gráficas completamente conectadas¶
A diferencia de las capas recurrentes, las capas de auto-atención no asumen una estructura (lineal) de los datos. Las capas de auto-atención interpretan los datos como parte de una gráfica completamente conectada.
Gráfica de entrada: El modelo de auto-atención asume una gráfica $G = (V, E)$ completamente conectada con un conjunto de vértices asociados a los vectores de entrada $x_1,...,x_n \in \mathbb{R}^d$.
Por ejemplo, podemos pensar en un conjunto de 4 tókens $w_0, w_1, w_2, w_3$. En principio, podemos asumir que todos los tókens se encuentran relacionados entre sí:
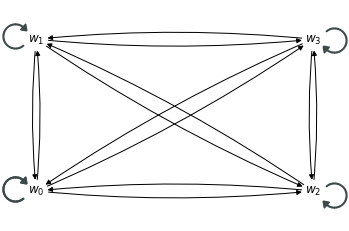
Sin embargo, es claro que, al menos, en el lenguaje natural no se dan este tipo de relaciones. Existen estructuras más complejas que definen relaciones entre los elementos de una cadena del lenguaje. Por ejemplo, dos tipos de relaciones manifestadas en gráficas sobre el lenguaje natural son los constituyentes inmediatos y las relaciones de dependencia:
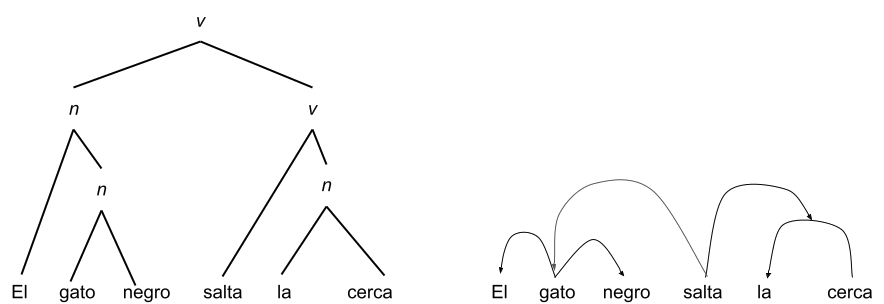
Por tanto, podemos asumir que existe una función de peso $\phi: E \to \mathbb{R}$ que asigna a cada arista de la gráfica $G$ un peso. Este peso puede interpretarse como una medida que cuantifica la relación entre los nodos representando a dos vectores $x_i$ y $x_j$, esta función de peso puede entenderse como los pesos de atención. Los pesos de atención determinan las relaciones entre los tókens de entreda, de tal forma que las representaciones de una cabeza de atención representan a las entradas con base en las relaciones que se establecen entre los tókens de entrada.
Clark et al. (2019) analizan el tipo de relaciones que aprenden las cabezas de auto-atención dentro del model BERT, que se basa en transformadores. Por ejemplo, en el siguiente caso se muestra que los pesos de atención capturan correferencias de anáforas:

De esta forma, los pesos de aención definen la matriz de adyacencia $A$ de la gráfica $G$ como:
$$A_{i,j} = \alpha(x_i, x_j)$$Esta matriz de adyacencia, los pesos de las conexiones entre los tókens de entrada, se estima a partir del entrenamiento de la red neuronal y depende del contexto de entrada. La matriz de pesos de atención, por tanto, puede variar según los elementos que se encuentren en la entrada, pero el objetivo es que los pesos de atención reflejen las relaciones subyacentes en los datos de entrada.
Por ejemplo, consideremos que tenemos una cadena de entrada "el gato negro salta la cerca" donde cada tóken corresponde a una palabra. Si asumimos que después de un proceso de entrenamiento la matriz de los pesos de atención es la siguiente:
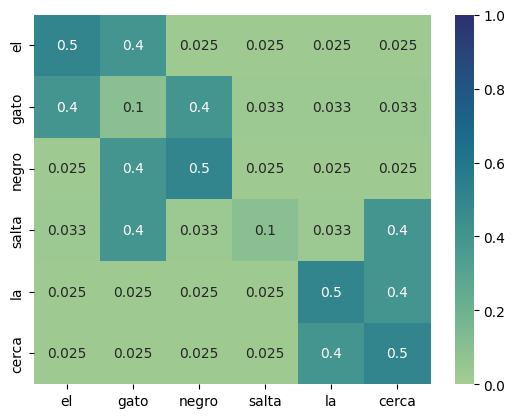
A partir de los pesos en esta matriz se generarán las representaciones de cada uno de los tókens de entrada. Por ejemplo, para la palabra "negro" se puede ver que los pesos más altos son los que corresponden a la misma palabra "negro" con 0.5 y a la palabra "gato" con 0.4. Esto nos dice que la representación de "negro" estará influenciada por la palabra "gato" con un peso de 0.4. Si desarrollamos la fórmula para obtener la representación $h_{negro}$ vemos que:
$$h_{negro} = 0.025 \cdot v_{el} + 0.4 \cdot v_{gato} + 0.5 \cdot v_{negro} + 0.025 \cdot v_{salta} + 0.025 \cdot v_{la} + 0.025 \cdot v_{cuerda}$$Donde cada $v_i$ es la proyección de la entrada en el espacio de valores. La matriz de pesos de atención, como señalabamos, también puede verse como una matriz de adyacencia. La matriz del ejemplo nos está diciendo que los elementos más relacionados con "negro" son sí mismos y "gato". Por tanto, podemos visualizar la matriz como una gráfica de la siguiente forma:
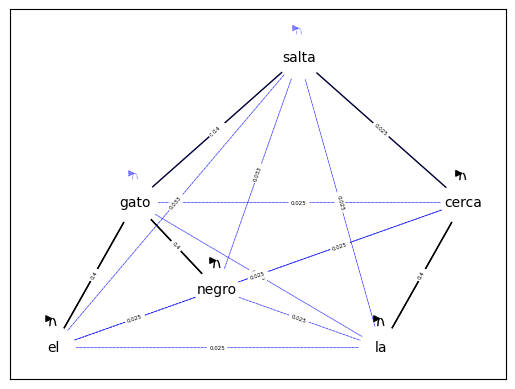
Las aristas más gruesas reflejan un peso más fuerte de los vecinos. Con estas relaciones, las representaciones que surgen de la auto-atención se estiman a partir de las relaciones con sus vecinos.
Visualmente, las representaciones obtenidas se acercan más a aquellos vectores con los que tienen un mayor peso de atención. Si retomamos el ejemplo de "negro", vemos que el vector resultado de la representación de la auto-atención se moverá hacia los vectores en el espacio de valores con los que tiene mayor peso, esto es hacia los vectores "negro" y "gato", ya que los pesos son cercanos a 0.5, el vector de la representación retultante quedará casi en medio de estos dos vectores de valores. Otro ejemplo es el vector representación para "gato" cuyos pesos se reparten mayormente entre "el" y "negro" por lo que su representación caerá casi entre estos dos vectores de valores.
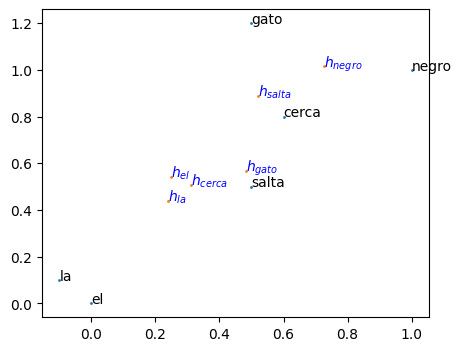
En la imagen podemos ver en negro los vectores en el espacio de valores, mientras que en azul $h_i$ representa a los vectores que resultan de la auto-atención. También se puede observar que las representaciones resultantes siempre quedan dentro del complejo convexo formado por los vectores en el espacio de valores.
Relación de auto-atención con otras redes gráficas¶
Bronstein et al. (2021) presentan una generalización de las capas de auto-atención y una teoría que relaciona la atención con otro tipos de capas. Dado que la auto-atención puede entenderse como una capa que interpreta una estructura de gráfica, se puede asumir que este tipo de capas puede tomar información de la conectividad de una gráfica para obtener información. De esta forma, la representación de un elemento $x_i$ con índice $i$ podría realizarse como:
$$h_i = \sum_{j \in \mathcal{N}_i} \alpha(x_i, x_j) \psi_v(x_j)$$En esta fórmula $\mathcal{N}_i$ son los vecinos de $x_i$ en una gráfica. Es decir, se suma únicamente por aquellos elementos que son vecinos al elemento actual. Si la gráfica es completamente conectada, se suma sobre todos los otros elementos y se tiene la capa de auto-atención típica.
Ahora supóngase que se tiene una gráfica en forma de cuadrícula, donde cada nodo puede identificarse con una coordenada $(i,j)$ y un nodo de esta forma se conecta con otro si es de la forma $(i-1, j), (i+1,j), (i,j-1)$ o $(i,j+1)$. La gráfica resultante es como la que se muestra a continuación:
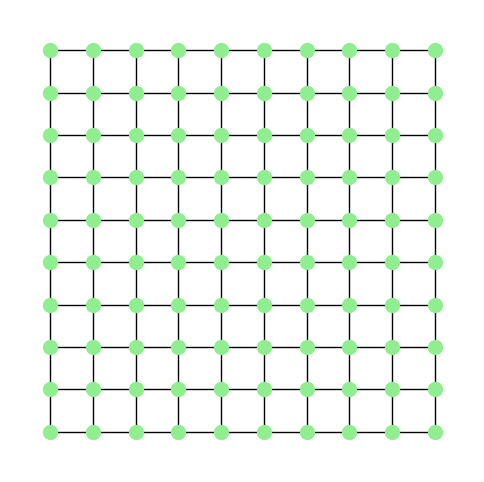
En este caso, la representación de un punto requiere sumar sobre sus vecinos; esto es, sobre los puntos que están alrededor (incluyendo al mismo punto) en la malla. De esta forma, obtener una representación en base a los vecinos puede verse como:
$$h_i = \sum_{j \in \mathcal{N}_i} \alpha(x_i, x_j) \psi_v(x_j) \\ ~ = \sum_{h} \sum_w \alpha(x_{i,j}, x_{i+h,j+w}) \psi_v(x_{i+h,j+w})$$Donde los índices $h$ y $w$ recorren a los vecinos del punto en la malla. Esta fórmula es similar a la de una red convolucional (con un kernel de $3\times 3$), sólo basta tomar $\alpha(x_i,x_{i+h,j+w}) = c_{h,w}$ con $c_{h,w}$ pesos del kernel y la transformación $\psi_v$ como la identidad. Así tendremos una representación como:
$$h_i = \sum_{h} \sum_w c_{h,w} x_{i+h,j+w}$$Que es la representación de una convolución, definido por un kernel con pesos $c_{h,w}$. De esta forma, Bronstein et al. (2021) señalan la relación que existe entre las redes convolucionales y las redes de auto-atención. Esta relación se presenta cuando se observa a la auto-atención como una red que asume una estructura de gráfica. Más aún, estos autores relacionan las redes atencionales con redes gráficas (específicamente con Message Passing):
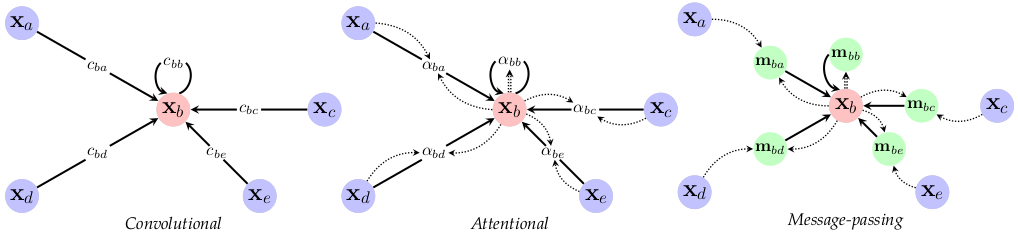
Las diferencias entre estos tres tipos de redes se dan en la forma en que pasan la información para obtener la representación de cada elemento de entrada. En las redes convolucionales, esta información pasa directamente desde los otros elementos multiplicando por cada peso del kernel $c_{h,w}$, mientras que en las redes atencionales se requiere de estimar los pesos de atención a partir del elemento actual y de su elemento vecino para después multiplicar el elemento vecino por este peso de atención. Finalmente, en las redes gráficas (