Atención dispersa

El proceso de enmascaramiento en la atención permite ignorar las relaciones de las tókens actuales con los tókens futuros. Podemos ver que está el enmascaramiento está ligado a la concepción de la atención como un mecanismo gráfico. En la atención enmascarada podemos suponer que tenemos una gráfica tal que un elemento $x_i$ está conectado con un elemento $x_j$ si y sólo si $j \leq i$, siendo $i$ y $j$ la posición absoluta de los tókens en la oración de entrada.

Child et al. (2019) proponen extender esta concepción todavía más para limitar las conexiones de los tókens actuales (y por tanto la información que pueden observar) a elementos que se encuentran en una posición determinada con respecto al elemento actual. Los autores proponer varias formas de conectar estos elementos con respecto a las relaciones de vecindad en la gráfica, de tal forma que se pueden determinar de manera específica las vecindades $\mathcal{N}_i$ de los elementos $x_i$. De tal forma, que la matriz de pesos de atención sólo tendrá valores en las entradas correspondientes a los elementos que están conectados entre sí y tendrá 0 en las otras entradas, funcionando como una matriz de adyacencia de una gráfica pesada. De la presencia de esto 0's es por lo que los autores llaman atención dispersa a este mecanismo.

En general, podemos pensar a la atención dispersa como un método de auto-atención en gráficas en donde se toma en cuenta sólo los elementos relacionados en una gráfica no necesariamente conectada por completo. Esto es:

$$h_i = \sum_{j \in\mathcal{N}_i} \alpha_(x_i, x_j) \psi_v(x_j)$$

Para simplificar el cálculo de la atención dispersa, empero, Child et al. (2019) proponen el uso de conexiones simples, que no requieran de la especificación explícita de una estructura de gráfica. Por ejemplo, los autores proponen algunos casos particulares que se muestran a continuación:

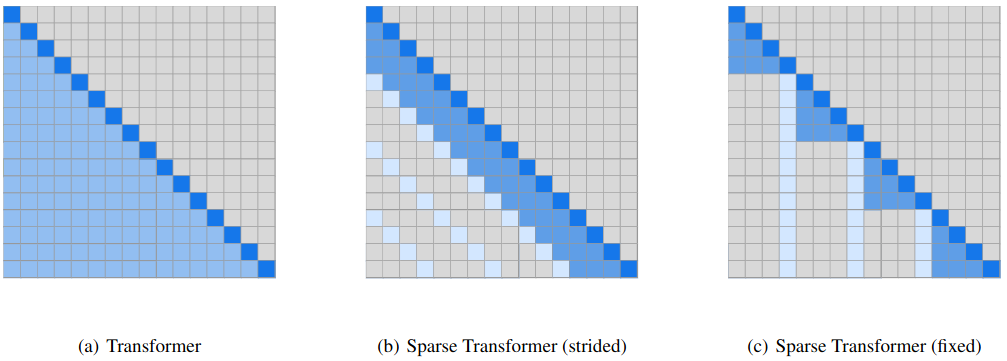
El caso más sencillo es el tomar en cuenta sólo los $k$ elementos anteriores al tóken actual. Es decir, en lugar de relacionar todos los anteriores, se tomará una ventana de tamaño $k$ para tomar los elementos. De esta forma, la representación de un elemento $x_i$ dependerá de la atención puesta sólo a los $k$ elementos anteriores, a esto le llaman stride attention. En la figura anterior (c) también se puede ver otra versión de atención fija. En este sentido, podemos definir la atención dispersa como sigue:

Atención dispersa: Es un mecanismo de auto-atención que genera matrices de atención dispersas, al considerar que las relaciones entre los datos de entrada $x_1, x_2,..., x_n$ no definen una gráfica completamente conectada. En particular, podemos definir la atención (Stride) dispersa, cuando las vecindades de los elementos están dadas como: $$\mathcal{N}_i = \{j : max(0, i-k) \leq j \leq i \}$$ Donde $k$ es un hiperparámetro que determina el número de elementos previos que se consideran.

Para la implementación de esta atención dispersa utilizaremos una máscara, pero tomando en cuenta el considerar sólo los $k$ elementos anteriores. El número $k$ de elementos previos que debemos considerar queda determinado como un hiperparámetro que llamamos stride. La implementación es similar a la auto-atención enmascarada, aunque tiende a ser más costosa la creación de la máscara.

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from seaborn import heatmap as hm
import numpy as np

class SparseAttention(nn.Module):
    #Atención enmascarando subsecuentes
    def __init__(self, d_model, stride=3):
        super(SparseAttention, self).__init__()
        self.d_model = d_model
        self.stride = stride
        self.Q = nn.Linear(d_model, d_model, bias=False)
        self.K = nn.Linear(d_model, d_model, bias=False)
        self.V = nn.Linear(d_model, d_model, bias=False)

    def forward(self, x):
        query, key, value = self.Q(x), self.K(x), self.V(x)
        scores = torch.matmul(query, key.T)/np.sqrt(self.d_model)
        #Enmascaramiento de los scores
        mask  = self.masking(x)
        scores = scores.masked_fill(mask == 0, -1e9)
        att = nn.functional.softmax(scores, dim=-1)
        h = torch.matmul(att, value)

        return h, att

    def masking(self, x):
        #Creación de la máscara
        n = x.size(0)
        mask = np.ones((n,n))
        for i in range(0,n):
            for j in range(0,self.stride):
                m = max(0,i-j)
                mask[i,m] = 0
        
        return torch.from_numpy(mask) == 0

Como podemos observar, el modelo de atención dispersa considerará sólo los $k$ elementos previos, ignorando los elementos subsiguientes y aquellos elementos previos que estén más allá de distancia $k$ al tóken actual. Si visualizamos la matriz de atención, podemos ver que la matriz será dispersa, conteniendo sólo valores de probabilidades en la diagonal y las $k$ entradas previas a ésta. Por ejemplo, si consideramos un stride igual a 3, estaremos asumiendo una estructura gráfica donde cada tóken conencta sólo con los 2 anteriores (y el mismo):

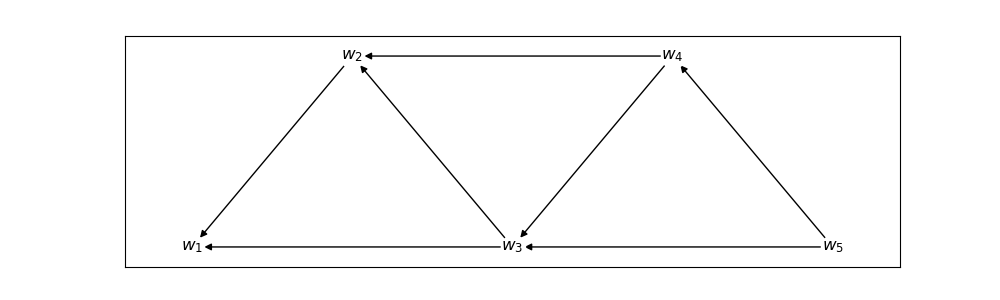
La matriz de atención sería como se muestra a continuación (donde todavía no se ha aprendido los pesos adecuados).

model = SparseAttention(128, stride=3)

x = torch.rand(5,128)
labels = ['$w_1$','$w_2$','$w_3$','$w_4$','$w_5$']
h, att = model(x)
hm(att.detach().numpy(), annot=True, xticklabels=labels, yticklabels=labels)
plt.show()

La atención dispersa, como lo proponen los Child et al. (2019), busca factorizar la atención para enfocarse en los llamados modelos autoregresivos que generen secuencias tanto de texto, como de imágenes o audio. La atención dispersa también busca disminuir la complejidad espacial de la atención común, pues es claro que una matriz de atención requiere de una complejidad $O(n^2)$ en memoria, mientras que con la atención dispersa, el uso de memoria (usando representaciones dispersas de las matrices de atención) se redice a orden $O(kn)$; Los autres proponen que $k \approx \sqrt{n}$. Sin embargo, la creación de la máscara puede tomar más tiempo, aumentando la complejidad temporal. Por ejemplo, en este caso la máscara se crea en tiempo $O(kn)$.

Aplicación de atención dispersa

Para aplicar la atención dispersa podemos utilizar el mismo ejemplo que hemos venido trabajando sobre un modelo del lenguaje. Utilizamos multi-cabezas, tomando en cada cabeza un tamaño de stride incremental, de tal forma que la primera cabeza sólo considera al elemento para la representación, la segunda cabeza considera al elemento anterior, la tercera a los dos elementos anteriores, etc. Este es el único cambo que introducimos en la implementación:

import copy

class MultiHeadMaskAttention(nn.Module):
    def __init__(self, in_size, d_model, hidden=128, heads=3, dropout=0.3):
        super(MultiHeadMaskAttention, self).__init__()
        self.d_model = d_model
        self.enc = Encoding(in_size, d_model)
        #Uso de atención dispersa con stride incremental
        self.att = nn.ModuleList([copy.deepcopy(SparseAttention(d_model, stride=i+1)) for i, _ in enumerate(range(heads))])
        self.lin = nn.Linear(heads*d_model, d_model, bias=True)
        self.norm = LayerNorm(d_model)
        self.ffw = nn.Sequential(nn.Linear(d_model, hidden), nn.ReLU(),
                                nn.Linear(hidden, d_model))
        self.drop1 = nn.Dropout(p=dropout)
        self.drop2 = nn.Dropout(p=dropout)
        self.drop3 = nn.Dropout(p=dropout)
    
    def forward(self, x):
        x_e = self.enc(x)
        x_e = self.drop1(x_e)
        head_att = [head(x_e) for head in self.att]
        self.att_weights = [head[1] for head in head_att]
        heads = [head[0] for head in head_att]
        multi_heads = torch.cat(heads, dim=-1)
        h = self.lin(multi_heads)
        h_norm = x_e + self.norm(h)
        h_norm = self.drop2(h_norm)
        out = self.ffw(h)
        
        return self.drop3(h_norm + self.norm(out))

Datos para el entrenamiento

Los datos de entrenamiento tienen las mismas características que anteriormente: se busca predecir la siguiente palabra, pero ahora el contexto de predicción será limitado por el tamaño del estride; sin embargo, debe notarse que esto no estima una probabilidad de ngramas, pues la información se transmite entre los diferentes elementos. Por ejemplo, si el stride es 3, entonces la representación del cuarto tóken $w_4$ dependerá de $w_3$ y $w_2$, pero no de $w_1$. Pero tanto la representación de $w_3$ y $w_2$ sí dependen de $w_1$ por lo que la información de este tóken se pasa de manera indirecta.

import pandas as pd
from tqdm import tqdm
from transformers import *

#Corpus a utilizar
corpus = ['el perro come un hueso', 'un muchacho jugaba', 'el muchacho saltaba la cuerda',
          'un perro come croquetas', 'el perro come', 'el gato come croquetas', 
          'un gato come', 'un muchacho jugaba con la cuerda', 'el muchacho jugaba con la cuerda']
corpus = [w.split() for w in corpus]
#Creación del vocabulario
voc = vocab()
voc['[bos]'] = 0
voc['[eos]'] = 1
#Indexación de cadenas
sents = list(index(corpus, voc))

#Pares de entrenamiento
x = [torch.cat((torch.tensor([voc['[bos]']]),s), axis=0) for s in sents]
y = [torch.cat((s, torch.tensor([voc['[eos]']])), axis=0) for s in sents]
print(x[0], y[0])

tensor([0, 2, 3, 4, 5, 6]) tensor([2, 3, 4, 5, 6, 1])

Entrenamiento del modelo

Ya con los datos de entrenamiento creados, podemos definir el modelo. Ya que en la arquitectura del modelo hemos determinado que el stride sea incremental en base al número de la cabeza, elejimos 4 cabezales para que el stride tome a lo más 4 elementos previos en la última cabeza.

len_voc = len(voc)
model = nn.Sequential(MultiHeadMaskAttention(len_voc, 128, heads=4), 
                      nn.Linear(128,len_voc), nn.Softmax(1)) 

#Carga del modelo
model.load_state_dict(torch.load('sparse.model'))
model.eval()

Sequential(
  (0): MultiHeadMaskAttention(
    (enc): Encoding(
      (emb): Embedding(15, 128)
      (pe): PositionalEncoding()
    )
    (att): ModuleList(
      (0-3): 4 x SparseAttention(
        (Q): Linear(in_features=128, out_features=128, bias=False)
        (K): Linear(in_features=128, out_features=128, bias=False)
        (V): Linear(in_features=128, out_features=128, bias=False)
      )
    )
    (lin): Linear(in_features=512, out_features=128, bias=True)
    (norm): LayerNorm()
    (ffw): Sequential(
      (0): Linear(in_features=128, out_features=128, bias=True)
      (1): ReLU()
      (2): Linear(in_features=128, out_features=128, bias=True)
    )
    (drop1): Dropout(p=0.3, inplace=False)
    (drop2): Dropout(p=0.3, inplace=False)
    (drop3): Dropout(p=0.3, inplace=False)
  )
  (1): Linear(in_features=128, out_features=15, bias=True)
  (2): Softmax(dim=1)
)

Ahora entrenamos el modelo con los datos de entrenamiento. Utilizamos el optimizador Noam que se revisará más adelante. Podemos guardar el modelo para cargarlo en posteriores pruebas.

criterion = nn.CrossEntropyLoss()
optimizer = NoamOptimizer(model.parameters(), model[0].d_model, decay=0.01)
epochs = range(100)

#Entrenamiento
model.train()
for t in tqdm(epochs):
    for i in torch.randperm(len(x)):
        prediction = model(x[i])
        optimizer.zero_grad()
        loss_value = criterion(prediction, y[i])
        loss_value.backward()
        optimizer.step()

#torch.save(model.state_dict(), 'model.model')

/home/cienciasia/anaconda3/lib/python3.11/site-packages/torch/cuda/__init__.py:619: UserWarning: Can't initialize NVML
  warnings.warn("Can't initialize NVML")
100%|█████████████████████████████████████████| 100/100 [00:09<00:00, 10.02it/s]

Exploración del modelo

Al igual que en otros ejemplos, podemos comenzar a explorar qué es lo que está aprendiendo el modelo; podemos observar las probabilidades de este modelo dado un contexto previo. Este tipo de modelos nos permitirá predecir una palabra siguiente que se adapta al contexto pevio. En el caso de la auto-atención enmascarada se toma todo los elementos previos para cada caso; aquí sólo se toman aquellos elementos que estén en la ventana para la representación. Esto puede tener cierta influencia en los cálculos de las probabilidades.

devoc = {i:t for t,i in voc.items()}
def result(text, model):
    #Función para predecir la siguiente palabra dado el contexto
    tokens = text.split()
    x = torch.tensor([voc[t] for t in tokens])
    pred = model(x)
    max_token = pred.argmax(axis=1).detach().numpy()
    
    return pred.detach().numpy(), ' '.join([devoc[i] for i in max_token])

p, pred_text = result('[bos]', model)
print('Palabra siguiente con mayor prob: {}'.format(pred_text))

#Visualización de probabilidades más altas
args = np.argsort(p[-1])[::-1]
probs = np.sort(p[-1])[::-1]
pd.DataFrame(data=probs, columns=['prob. tóken'], index=[devoc[j] for j in args]).plot.bar()
plt.show()

Palabra siguiente con mayor prob: el

Finalmente, nuestro interés radica en explorar el tipo de matrices de atención que se están obteniendo. Como lo deciamos, hemos definido un stride incremental, por lo que la primera cabeza tendrá una matriz diagonal. En este caso, realmente no se está haciendo un proceso de atención, pues el elemento se está representando sólo por sí mismo o, de forma más específica, por su proyección en el espacio de valores; es decir, tenemos que: $h_i = \psi_v(x_i)$ con un peso de atención de probabilidad 1. Los otros casos son más interesante, pues en la segunda cabeza, cada elemento se representará por sí mismo y el elemento anterior. En este caso particular, parece que todos las probabilidades de los pesos de atención son cercanas a $\frac{1}{2}$; es decir, cada elemento se representa con la información tanto de sí mismo como del elemento anterior por igual. En la cabeza 3 se representará por los 2 elementos anteriores, y finalmente en la cabeza 4 se representará por los 4 elementos anteriores, que en el ejemplo particular que aquí usamos corresponde a todos los elementos previos.

text = '[bos] un gato come'
result(text, model)

for i, att_w in enumerate(model[0].att_weights):
    hm(att_w.detach().numpy(), xticklabels=text.split(), yticklabels=text.split(), vmin=0, vmax=1)
    plt.title('Atención en cabeza %i' %i)
    plt.show()

Referencias

Child, R., Gray, S., Radford, A., & Sutskever, I. (2019). Generating long sequences with sparse transformers. arXiv preprint arXiv:1904.10509.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.

---

Principal