Suma y normalización¶
Vaswani et al. (2018), cuando proponen la arquitectura del tranformador, proponen utilizar una normalización y capas residuales por cada capa que se computa dentro de la arquitectura. Para empezar a construir la arquitectura del transformado, se consideran las siguientes capas:
- Capa de embedding y codificación posicional: dónde cada tóken de entrada se convierte en un vector que lo representa y se agrega su información posicional.
- Auto-atención: Obtiene representaciones a partir de una suma convexa de las representaciones del contexto.
- Suma y normalización: Realiza una normalización a los vectores y suma las representaciones de la capa previa.
- Feedforward: Aplica una red feedforward a los datos para obtener una representación final de estos.
Las primeras dos capas ya han sido revisadas, y ahora revisamos las siguientes capas. Estas capas no conforman toda la arquitectura del transformador, se orientan al módulo del codificador, pero servirán para entender la arquitectura completa de este modelo. El diagrama que seguimos es el siguiente:
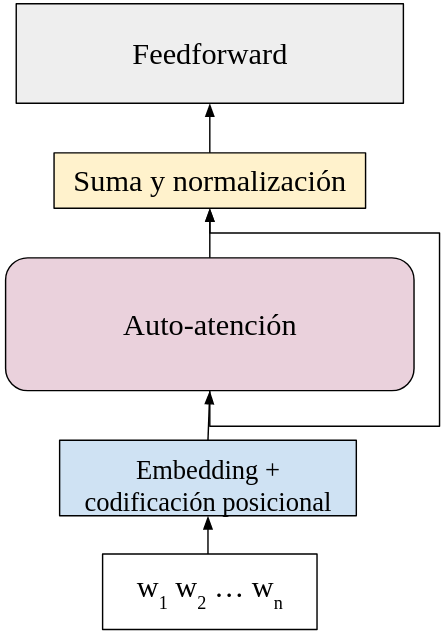
Normalización¶
La normalización que se realiza en los transformadores es la normalización por lotes. Este tipo de normalización tiene bases estadísticas y busca solucionar el problema del cambio interno de covarianza:
Problema del cambio interno de covarianza: Se entiende como el cambio en las activaciones de la red debido al cambio de los parámetros de la red neuronal durante el entrenamiento.
Estos cambios pueden darse debido a que la distribución de los diferentes lotes de datos con los que se entrenan pueden tener una distribución diferente. Para solventar el problema del cambio interno de covarianza se propone una normalización. La normalización lleva la distribución de los datos del lote a una media 0 y a hacia una varianza 1. Esta normalización se realiza como:
$$\hat{x} = \frac{x-\mu}{\sqrt{\sigma^2} + \epsilon}$$Donde $\mu_x$ es la media sobre cada dimensión de los datos $x$, $\sigma^2$ es la varianza y $\epsilon$ es una valor pequeño que evita la división entre 0. La media y la varianza se estiman de la forma común como:
$$\mu = \frac{1}{N}\sum_{i=1}^N x_i \\ \sigma^2 = \frac{1}{N-1} \sum_i (x_i - \mu)^2$$Donde $x_i$, $i=1,2,...,N$, son cada uno de los datos del lote. Puede comprobarse fácilmente que la media de los datos normalizados $\hat{x}$ es 0 y su varianza es 1 (o cercana a 1, dependiendo del factor $\epsilon$). Sin embargo, Ioffe y Szegedy (2015) señalan que esta normalización sola puede cambiar lo que una capa puede representar. Para lidiar con esto, proponen regular la normalización con dos parámetros $a$ y $b$ que se aprenden dentro del mismo modelo; de tal forma que la normalización por lote se da como:
$$\hat{x} = a \odot \frac{x-\mu}{\sqrt{\sigma^2} + \epsilon} + b$$Donde $\odot$ señala un producto punto a punto. La normalización propuesta amortigua el problema del cambio interno de covarianza y, en general, permite un mejor entrenamiento, sobre todo cuando se cuenta con arquitecturas grandes que entrenan con cantidades también grandes de datos.
La implementación de la normalización se realizará de la siguiente forma:
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a = nn.Parameter(torch.ones(features))
self.b = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a*(x - mean)/(std + self.eps) + self.b
En este caso se toma un valor de $\epsilon = 1e-6$.
Capas residuales¶
Las capas residuales consisten en agregar a una capa actual capas previas que no son inmediatamente anteriores. De esta forma, la información de las capas no inmediatamente previas se agrega a la capa actual. En la figura superior, la conexión residual se muestra como una flecha que se salta una de las capas. En el caso de los transformadores se suman las representaciones de las capas previas que no son inmediatamente anteriores. Vaswani et al. (2018) proponen que esta suma se realice como:
$$h = x + capa\big( norm(x) \big)$$En esta formulación capa refiere a la aplicación de la capa previa y norm a la normalización por lotes. De esta forma, la normalización y la suma por cada capa llevaría a que el módulo del transformador sea de la siguiente forma:
$$h = x + ffw\Big(norm\big( x + att(norm(x)) \big) \Big)$$En donde ffw es la feedforward y att es la capa de auto-atención. En contraste con esto, Chowdhery et al. (2022) proponen aplicar la suma y normalización como:
$$h = x + ffw\big(norm(x)\big) + att\big(norm(x)\big)$$Donde, en lugar de trabajar con las capas de forma secuencial, se realiza la normalización en cada capa y se suman las capas. Los autores señalan que esto permite una paralización de la suma y normalización. La implementación que aquí mostramos es secuencial:
class Residual(nn.Module):
def __init__(self, size):
super(Residual, self).__init__()
self.norm = LayerNorm(size)
def forward(self, x, layer):
return x + layer(self.norm(x))
De esta forma, el módulo expuesto aplicará la suma y la normalización para los transformadores. Aquí layer refiere a la capa actual a la que se aplicará la suma y normalización.