TransformadorΒΆ
La arquitectura original de un transformador es una arquitectura encoder-decoder, cuenta con dos grandes secciones en donde la primera, el encoder, toma la cadena de entrada y la codifica a travΓ©s de un mecanismo de auto-atenciΓ³n para pasar los datos codificados a un decoder, la segunda secciΓ³n del transformador, que se encargarΓ‘ de decodificar estos datos en una nueva cadena. Como puede imaginarse, los transformadores son de gran utilidad para la traducciΓ³n automΓ‘tica y otras tareas que pasan de secuencia a secuencia.
Los transformadores han tenido un gran impacto en el procesamiento del lenguaje natural, pues permiten obtener modelos de gran capacidad que, ademΓ‘s, son capaces de generar lenguaje de manera efectiva. Para poder definir la arquitectura del transformador definimos el encoder y el decoder; para este ΓΊltimo requerimos de un mecanismo de atenciΓ³n que tome tanto la cadena de entrada como la cadena de salida.
AtenciΓ³n encoder-decoderΒΆ
Al igual que los modelos de atenciΓ³n en las redes recurrentes encoder-decoder, los transformadores utilizan una atenciΓ³n que representa los elementos de la salida a partir de los datos de entrada, para poner atenciΓ³n a aquellos elementos de entrada que tengan mΓ‘s influencia en la salida actual. En este caso, se toma una query que es elemento de la salida. Supongamos que tenemos una cadena de entrada $x_1, x_2, \cdots x_n$ que se mapea en una cadena de salida $y_1, y_2, \cdots y_m$, entonces buscaremos obtener una representaciΓ³n de los elementos de salida $y_1, y_2, \cdots y_m$ en tΓ©rminos de la entrada $x_1, x_2, \cdots x_n$. Esta representaciΓ³n pondrΓ‘ "atenciΓ³n" a los elementos de entrada:
$$h^y_i = \sum_{j=1}^n \alpha(y_i, x_j) \psi_v(x_j)$$Se obtendrΓ‘n las representaciones para los $m$ elementos de salida. AquΓ cabe decr que $\psi_v(x_j) = W_v x_j$ es una proyecciΓ³n en el espacio de valores de los datos de entrada y los pesos de atenciΓ³n se estiman de manera similar, peroconsiderando que los elementos $x_j$ corresponden a las entradas y $y_i$ a las salidas. De tal forma que estos pesos de atenciΓ³n se estiman como:
$$\alpha(y_i, x_j) = Softmax_x\Big( \frac{\psi_q(y_i)^T \psi_k(x_j)}{\sqrt{d}} \Big)$$La funciΓ³n $\psi_q(y_i) = W_q y_i$ es una proyecciΓ³n al espacio de queries de los valores de las salidas, mientras que $\psi_k(x_j) = W_k x_j$ es la proyecciΓ³n al espacio de keys de las codificaciones de entrada. De tal forma que la matriz de pesos de atenciΓ³n muestra las relaciones entre la entrada y la salida:
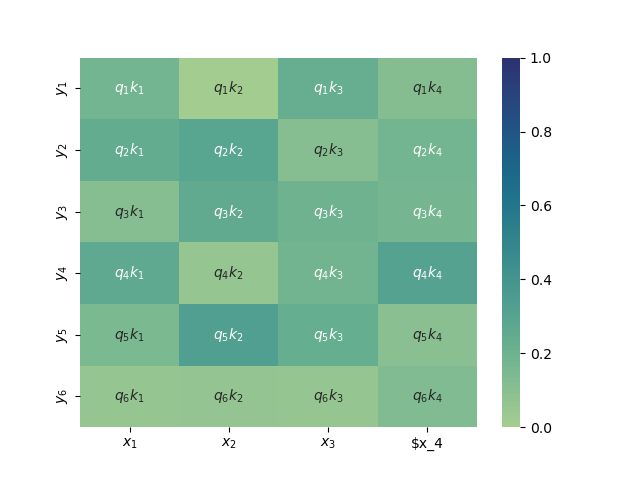
La atenciΓ³n entre el encoder y el decoder es similar a la auto-atenciΓ³n que se usa en cada mΓ³dulo, pero toma como valores de entrada $x_1, x_2, \cdots, x_n$ a las salidas del decoder, que ya han sido representados por medio de la auto-atenciΓ³n. Asimismo, toma los tΓ³kens de salida que tmabiΓ©n representa por medio de auto-atenciΓ³n (enmascarada). En la implementaciΓ³n de esta atenciΓ³n llamamos encode a los elementos codificados del encoder.
import torch
import torch.nn as nn
import numpy as np
import copy
from tqdm import tqdm
from transformers import *
class Attention(nn.Module):
def __init__(self, d_model):
super(Attention, self).__init__()
# Capas de proyecciones
self.d_model = d_model
self.Q = nn.Linear(d_model, d_model, bias=False)
self.K = nn.Linear(d_model, d_model, bias=False)
self.V = nn.Linear(d_model, d_model, bias=False)
def forward(self, x, encode):
# ProyecciΓ³n de los datos
query,key,value = self.Q(x),self.K(encode),self.V(encode)
scores = torch.matmul(query, key.T)/np.sqrt(self.d_model)
p_attn = torch.nn.functional.softmax(scores, dim = -1)
Vs = torch.matmul(p_attn, value).reshape(x.shape)
return Vs, p_attn
EncoderΒΆ
El encoder codifica la cadena de entrada en un conjunto de vectores con que se alimentarΓ‘ el decoder para obtener las salidas. Para hacer esta codificaciΓ³n, la arquitectura que se toma cuenta con: 1) embeddings y codificaciΓ³n posicional; 2) auto-atenciΓ³n multi-cabeza; y 3) capa feedforward. AdemΓ‘s aplica sum ay normalizaciΓ³n en cada capa. La siguiente figura expresa esta estructura:
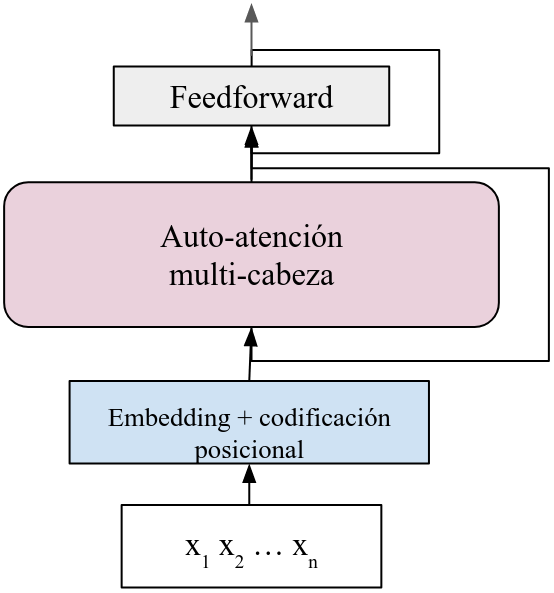
En el diagrama las conexiones que saltan capas representan la suma y normalizaciΓ³n. Definimos la implementaciΓ³n del encoder de manera similar que lo hemos hecho en la definiciΓ³n de las cabezas de auto-atenciΓ³n.
class Encoder(nn.Module):
def __init__(self, in_size, d_model, hidden=128, heads=3, dropout=0.3):
super(Encoder, self).__init__()
self.d_model = d_model
self.enc = Encoding(in_size, d_model)
self.att = nn.ModuleList([copy.deepcopy(SelfAttention(d_model)) for _ in range(heads)])
self.lin = nn.Linear(heads*d_model, d_model, bias=True)
self.norm = LayerNorm(d_model)
self.ffw = nn.Sequential(nn.Linear(d_model, hidden), nn.ReLU(),
nn.Linear(hidden, d_model))
self.drop1 = nn.Dropout(p=dropout)
self.drop2 = nn.Dropout(p=dropout)
self.drop3 = nn.Dropout(p=dropout)
def forward(self, x):
x_e = self.enc(x)
x_e = self.drop1(x_e)
head_att = [head(x_e) for head in self.att]
self.att_weights = [head[1] for head in head_att]
heads = [head[0] for head in head_att]
multi_heads = torch.cat(heads, dim=-1)
h = self.lin(multi_heads)
h_norm = x_e + self.norm(h)
h_norm = self.drop2(h_norm)
out = self.ffw(h)
return self.drop3(h_norm + self.norm(out))
DecoderΒΆ
El decoder es particular; suarquitectura es mΓ‘s compleja pero tambiΓ©n guarda similitudes con la del encoder, pues la cadena de salida pasa por las siguientes capas: 1) embedding y codificaciΓ³n posicional; 2) auto-atenciΓ³n enmascarada; y 3) capa feedforward, ademΓ‘s de la suma y normalizaciΓ³n. En primer lugar, la auto-atenciΓ³n que se utiliza es enmascarada, pues se puede ver que en la etapa de inferencia, cuando predecimos cadenas que no han sido vistas previamente, se busca generar una nueva cadena a partir de predecir la palabra siguiente. Por tanto, aquΓ es necesario enmascarar los tΓ³kens subsiguientes en la cadena.
Durante el entrenamiento, contamos con los pares $(\mathbf{x}, \mathbf{y})$ donde conocemos la cadena de salida. Por tanto, podemos aplicar las primeras tres capas de forma similar a como se ha mostrado en la secciΓ³n de auto-atenciΓ³n enmascarada. En este caso, no habrΓ‘ problema en la predicciΓ³n. Sin embargo en la inferencia requeriremos otra estrategia para generar los tΓ³kens de salida.
El decoder, ademΓ‘s de estas capas, incorporarΓ‘ una capa de atenciΓ³n (generalmente tambiΓ©n multi-cabeza) como la que hemos descrito arriba, donde tomarΓ‘ las codificaciones de la entrada y las utilizarΓ‘ para crear las representaciones de la salida a partir del mecanismo de atenciΓ³n. El siguiente diagrama muestra la estructura del decoder:
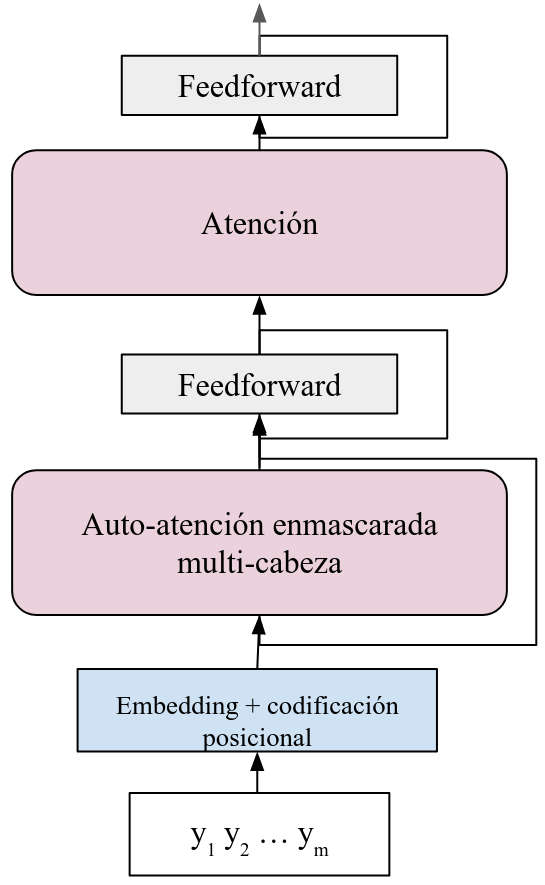
Cabe seΓ±alar que la capa de auto-atenciΓ³n no sΓ³lo toma la salida de la capa previa de auto-atenciΓ³n enmascarada, la que conforma el query, sino que toma la salida del encoder para conformar key y value. En este caso, debemos enviar al decoder los elemntos del decoder para que pueda trabajarlos.
class Decoder(nn.Module):
def __init__(self, in_size, d_model, hidden=128, heads=3, dropout=0.3):
super(Decoder, self).__init__()
self.d_model = d_model
self.enc = Encoding(in_size, d_model)
self.self_att = nn.ModuleList([copy.deepcopy(MaskAttention(d_model)) for _ in range(heads)])
self.att = Attention(d_model)
self.lin = nn.Linear(heads*d_model, d_model, bias=True)
self.norm = LayerNorm(d_model)
self.ffw1 = nn.Sequential(nn.Linear(d_model, hidden), nn.ReLU(),
nn.Linear(hidden, d_model))
self.ffw2 = nn.Sequential(nn.Linear(d_model, hidden), nn.ReLU(),
nn.Linear(hidden, d_model))
self.drop1 = nn.Dropout(p=dropout)
self.drop2 = nn.Dropout(p=dropout)
self.drop3 = nn.Dropout(p=dropout)
def forward(self, x, encode):
x_e = self.enc(x)
x_e = self.drop1(x_e)
head_att = [head(x_e) for head in self.self_att]
self.att_weights = [head[1] for head in head_att]
heads = [head[0] for head in head_att]
multi_heads = torch.cat(heads, dim=-1)
h = self.lin(multi_heads)
h_norm = x_e + self.norm(h)
h_norm = self.ffw1(h_norm)
h_norm = h + self.norm(h_norm)
h_norm = self.drop2(h_norm)
enc_dec, self.enc_dec_att = self.att(h_norm, encode)
enc_dec = h_norm + self.norm(enc_dec)
out = self.ffw2(enc_dec)
return self.drop3(h_norm + self.norm(out))
Encoder-decoderΒΆ
Ya que hemos definido de manera separada el encoder y el decoder, la arquitectura final incorporarΓ‘ ambos conectando la salida del encoder con la atenciΓ³n en el decoder que, ademΓ‘s, toma la salida de la representaciΓ³n como query. El resultado de esta ΓΊltima aplicaciΓ³n de la atenciΓ³n entre los elementos del encoder y del decoder pasarΓ‘ por una capa feedforward (ademΓ‘s de la suma y normalizaciΓ³n) para obtener las representaciones finales. Finalmente, para obtener las probabilidades de salida para las predicciones aplicamos una capa lineal y una activaciΓ³n con la funciΓ³n Softmax. De esta forma, obtendremos probabilidades de una cadena de salida con la que podremos hacer predicciones. El siguiente diagrama expresa la arquitectura del transformer.
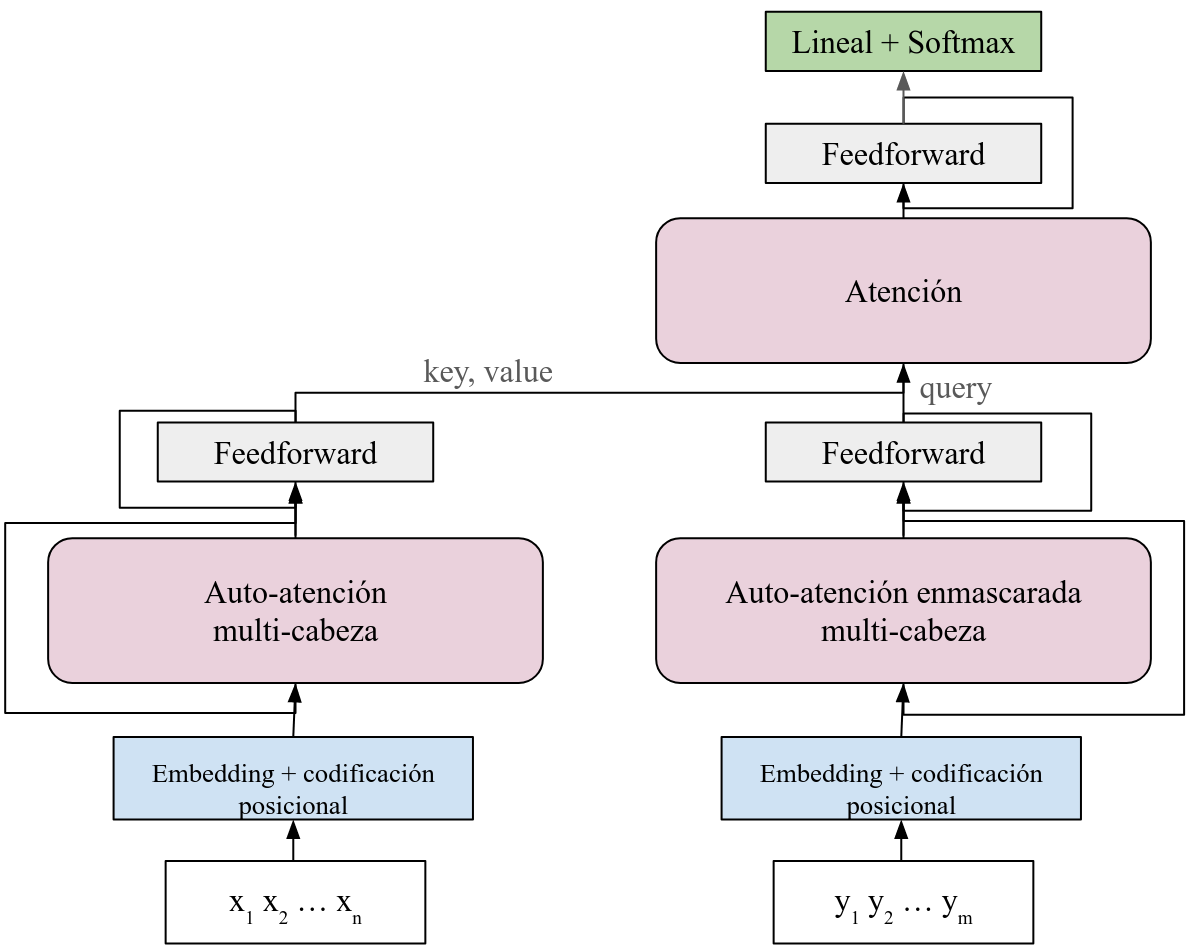
Cabe seΓ±alar que originalmente Vaswani et al. (2017) proponen que se creen copias tanto del encoder, como del decoder. En este cado, no aplicamos estas copias, sΓ³lo utilizamos un encoder y un decoder. Asimismo, no hemos declarado multi-cabezas en la atenciΓ³n entre el encoder y el decoder, esto con motivos de simplificar la implementaciΓ³n. En esta implementaciΓ³n ademas definimos funciones de encode y decode que utilizaremos para la inferencia.
class EncoderDecoder(nn.Module):
def __init__(self, in_size, out_size, d_model, hidden=128, heads=5, dropout=0.3):
super(EncoderDecoder, self).__init__()
self.d_model = d_model
self.encoder = Encoder(in_size, d_model, hidden=hidden, heads=heads, dropout=dropout)
self.decoder = Decoder(out_size, d_model, hidden=hidden, heads=heads, dropout=dropout)
self.generator = nn.Sequential(nn.Linear(d_model, out_size), nn.Softmax(1))
def forward(self, x, y):
enc = self.encode(x)
out = self.decode(y, enc)
return out
def encode(self, x):
return self.encoder(x)
def decode(self, x, encode):
return self.generator(self.decoder(x, encode))
AplicaicΓ³n del transformadorΒΆ
Para ejemplificar el uso del transformador definimos un problema de traducciΓ³n del espaΓ±ol al otomΓ. Utilizamos un corpus paralelo que obtenemos a partir de la paqueterΓa de Elotl. En este caso, generamos un vocabulario para el lenguaje fuente y el lenguaje objetivo, y asignamos Γndices a cada tΓ³ken/palabra para poder indexar estas palabras en las cadenas que se van a traducir.
import elotl.corpus
import matplotlib.pyplot as plt
from seaborn import heatmap as hm
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
corpus_ot = elotl.corpus.load('tsunkua')
src, tgt = zip(*[(sents[0].lower().split(), sents[1].lower().split()) for sents in corpus_ot])
bos = 0
eos = 1
src_voc = vocab()
tgt_voc = vocab()
src_voc['bos'], tgt_voc['bos'] = bos, bos
src_voc['eos'], tgt_voc['eos'] = eos, eos
src_sents = list(index(src, src_voc))
tgt_sents = list(index(tgt, tgt_voc))
x = [torch.cat((torch.tensor([src_voc['[bos]']]),s, torch.tensor([src_voc['[eos]']])), axis=0).to(device) for s in src_sents]
y = [torch.cat((torch.tensor([tgt_voc['[bos]']]),s, torch.tensor([tgt_voc['[eos]']])), axis=0).to(device) for s in tgt_sents]
#print(src_voc, tgt_voc)
Ahora generamos el modelo especificando el tamaΓ±o de vocabulario de entrada y el de salida. Definimos la dimensiΓ³n del modelo y podemos considerar otros hiperparΓ‘metros si es necesario.
len_src = len(src_voc)
len_tgt = len(tgt_voc)
model = EncoderDecoder(in_size=len_src, out_size=len_tgt, d_model=128, hidden=256).to(device)
#Carga del mo"delo
model.load_state_dict(torch.load('transformer.model', map_location=torch.device('cpu')))
model.eval()
EncoderDecoder(
(encoder): Encoder(
(enc): Encoding(
(emb): Embedding(4044, 128)
(pe): PositionalEncoding()
)
(att): ModuleList(
(0-4): 5 x SelfAttention(
(Q): Linear(in_features=128, out_features=128, bias=False)
(K): Linear(in_features=128, out_features=128, bias=False)
(V): Linear(in_features=128, out_features=128, bias=False)
)
)
(lin): Linear(in_features=640, out_features=128, bias=True)
(norm): LayerNorm()
(ffw): Sequential(
(0): Linear(in_features=128, out_features=256, bias=True)
(1): ReLU()
(2): Linear(in_features=256, out_features=128, bias=True)
)
(drop1): Dropout(p=0.3, inplace=False)
(drop2): Dropout(p=0.3, inplace=False)
(drop3): Dropout(p=0.3, inplace=False)
)
(decoder): Decoder(
(enc): Encoding(
(emb): Embedding(3599, 128)
(pe): PositionalEncoding()
)
(self_att): ModuleList(
(0-4): 5 x MaskAttention(
(Q): Linear(in_features=128, out_features=128, bias=False)
(K): Linear(in_features=128, out_features=128, bias=False)
(V): Linear(in_features=128, out_features=128, bias=False)
)
)
(att): Attention(
(Q): Linear(in_features=128, out_features=128, bias=False)
(K): Linear(in_features=128, out_features=128, bias=False)
(V): Linear(in_features=128, out_features=128, bias=False)
)
(lin): Linear(in_features=640, out_features=128, bias=True)
(norm): LayerNorm()
(ffw1): Sequential(
(0): Linear(in_features=128, out_features=256, bias=True)
(1): ReLU()
(2): Linear(in_features=256, out_features=128, bias=True)
)
(ffw2): Sequential(
(0): Linear(in_features=128, out_features=256, bias=True)
(1): ReLU()
(2): Linear(in_features=256, out_features=128, bias=True)
)
(drop1): Dropout(p=0.3, inplace=False)
(drop2): Dropout(p=0.3, inplace=False)
(drop3): Dropout(p=0.3, inplace=False)
)
(generator): Sequential(
(0): Linear(in_features=128, out_features=3599, bias=True)
(1): Softmax(dim=1)
)
)
EntrenamientoΒΆ
Para el entrenamiento utilizamos lotes de tamaΓ±o 1, es decir, pasamos ejemplo por ejemplo, pero es posible crear lotes de mayor tamaΓ±o. Como funciΓ³n objetivo utilizamos la entropΓa cruzada, pues nuestra funciΓ³n de salida es la funciΓ³n Softmax que obtiene probabilidades. El optizador es el optimizador Noam y entrenamos de forma comΓΊn por un nΓΊmero $T$ de iteraciones.
criterion = nn.CrossEntropyLoss()
optimizer = NoamOptimizer(model.parameters(), model.d_model, decay=0)
epochs = range(100)
#Entrenamiento
model.train()
for t in tqdm(epochs):
for i in torch.randperm(len(x)):
prediction = model(x[i], y[i])
optimizer.zero_grad()
loss_value = criterion(prediction, y[i])
loss_value.backward()
optimizer.step()
#torch.save(model.state_dict(), 'transformer.model')
InferenciaΒΆ
Para realizar la predicciΓ³n de nuevas cadenas a partir de datos novedosos de traducciΓ³n, definimos un decodificador ambicioso, que es un simple decodificador que en cada tiempo tomar el tΓ³ken con la probabilidad mΓ‘s alta como el tΓ³ken siguiente. Este tΓ³ken se incorpora a la cadena predica para volver a estimar otra palabra aplicando el decoder. Como se puede ver en el cΓ³digo, el encoder se aplica una sola vez (utilizamos la funciΓ³n encode), mientras que el decoder se aplica tantas veces como la longitud de la cadena de salida. En cada paso se incopora la palabra predicha anteriormente. Al inicio sΓ³lo tomamos el sΓmbolo de inicio de palabra. De esta forma, se puede predecir una cadena de longitud arbtrario para la salida del transformador. Asimismo, definimos funciones auxiliares que nos permitirΓ‘n pasar de las palabras en los lenguajes de entrada y salida a Γndices y viceversa.
model.eval()
def greedy_decode(model, x, max_len, start_symbol):
encode = model.encode(x)
ys = torch.ones(1).fill_(start_symbol).type_as(x.data)
for i in range(max_len-1):
prob = model.decode(ys, encode)
_, next_word = torch.max(prob, dim = 1)
next_word = next_word[-1].reshape(1)
ys = torch.cat((ys, next_word), dim=0)
return ys
tgt_voc_rev = {k:v for v,k in tgt_voc.items()}
def translate(sent, model, max_len=10):
x_sents = []
for w in sent.split():
idx_w = src_voc[w]
x_sents.append(idx_w)
x_sents = [bos] + x_sents + [eos]
y = greedy_decode(model, torch.tensor(x_sents).to(device), max_len, bos)
sent = y.cpu().detach().tolist()
return ' '.join([tgt_voc_rev[word] for word in sent][1:])
Finalmente, podemos obtener el resultado de traducciΓ³n de un texto. Ya que sΓ³lo hemos definido una cabeza de atenciΓ³n entre el encoder y el decoder podemos visualizar cuΓ‘les son los pesos aprendidos. TambiΓ©n se pueden visualizar los pesos de atenciΓ³n tanto en el encoder, como en el decoder (auto-atenciΓ³n enmascarada).
text = 'se calcina su piel'
result = translate(text, model, max_len=len(text.split())+1)
print('Original: {}\nTraducciΓ³n: {}'.format(text,result))
hm(model.decoder.enc_dec_att.cpu().detach().numpy(), xticklabels=['bos']+text.split()+['eos'],
yticklabels=result.split(), vmin=0, vmax=1)
plt.title('Pesos de atenciΓ³n en transformador')
plt.show()
Original: se calcina su piel TraducciΓ³n: xbi hΓ±Γ€hΓ±u. hokagihe nge'uΜ±
for i,att in enumerate(model.encoder.att_weights):
hm(att.cpu().detach().numpy(), xticklabels=['bos']+text.split()+['eos'],
yticklabels=['bos']+text.split()+['eos'], vmin=0, vmax=1)
plt.title('Auto-atenciΓ³n del encoder')
plt.show()
for i,att in enumerate(model.decoder.att_weights):
hm(att.cpu().detach().numpy(), xticklabels=result.split(),
yticklabels=result.split(), vmin=0, vmax=1)
plt.title('Auto-atenciΓ³n del decoder')
plt.show()
ReferenciasΒΆ
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017).